从FIPS 46-3中理解DES算法

tcc0lin 收录于类别加密算法研究

2023-05-09 2023-05-09 约 3358 字预计阅读 15 分钟

警告

本文最后更新于 2023-05-09，文中内容可能已过时。

DES是一种对称密钥的块加密算法。”对称密钥”，是因为加密、解密用的密钥是一样的（这不同于RSA等非对称密钥体系）。“块加密”，是因为这种算法把明文划分为很多个等长的块(block)，对每个块进行加密，最后以某种手段拼在一起。“块加密”亦称“分组加密”。

1973年，NSA向社会征集满足安全要求的加密算法。1973-1974年，IBM研发了DES加密算法。1974年，NSA开始了第二次征集，此后DES在1976年成为美国联邦标准。

一、DES概述

DES的功能是：给定一个64位的明文和一个64位的密钥，输出一个64位的密文。这个密文可以用相同的密钥解密。所谓“64位的密钥”，其实里面只有54位在起作用。剩余的位可以直接丢弃，或者当作奇偶校验位。

虽然DES一次只能加密8个字节，但我们只需要把明文划分成每8个字节一组的块，就可以实现任意长度明文的加密。如果明文长度不是8个字节的倍数，还得进行填充。现在流行的填充方式是PKCS7/PKCS5，都是很简单的思路，用于把任意长度的文本填充成8字节的倍数长，也能方便地恢复原文，这里不再赘述。此外，独立地对每个块加密，最后直接拼起来是不行的（这种方式称为“电子密码本”，ECB模式。它会导致明文中重复的块，加密结果也重复，这对于图片之类的数据来说几乎是致命的）。因为不涵盖在算法流程中，因此对有关DES输入输出的处理后续再讲。

DES有一个非常不平凡的性质——加密与解密算法几乎一模一样。这大大简化了软件和硬件的设计。和加密算法的区别是，给它加上一行（倒转子密钥的顺序），就是一个解密算法了。

在这篇文章中，我们只关注一个核心任务——如何把64位的明文，用64位的密钥，加密成64位的密文，并执行解密。

二、DES算法框架

DES算法是在Feistel Network（费斯妥网络）的基础上执行的。以下是DES算法的流程图：

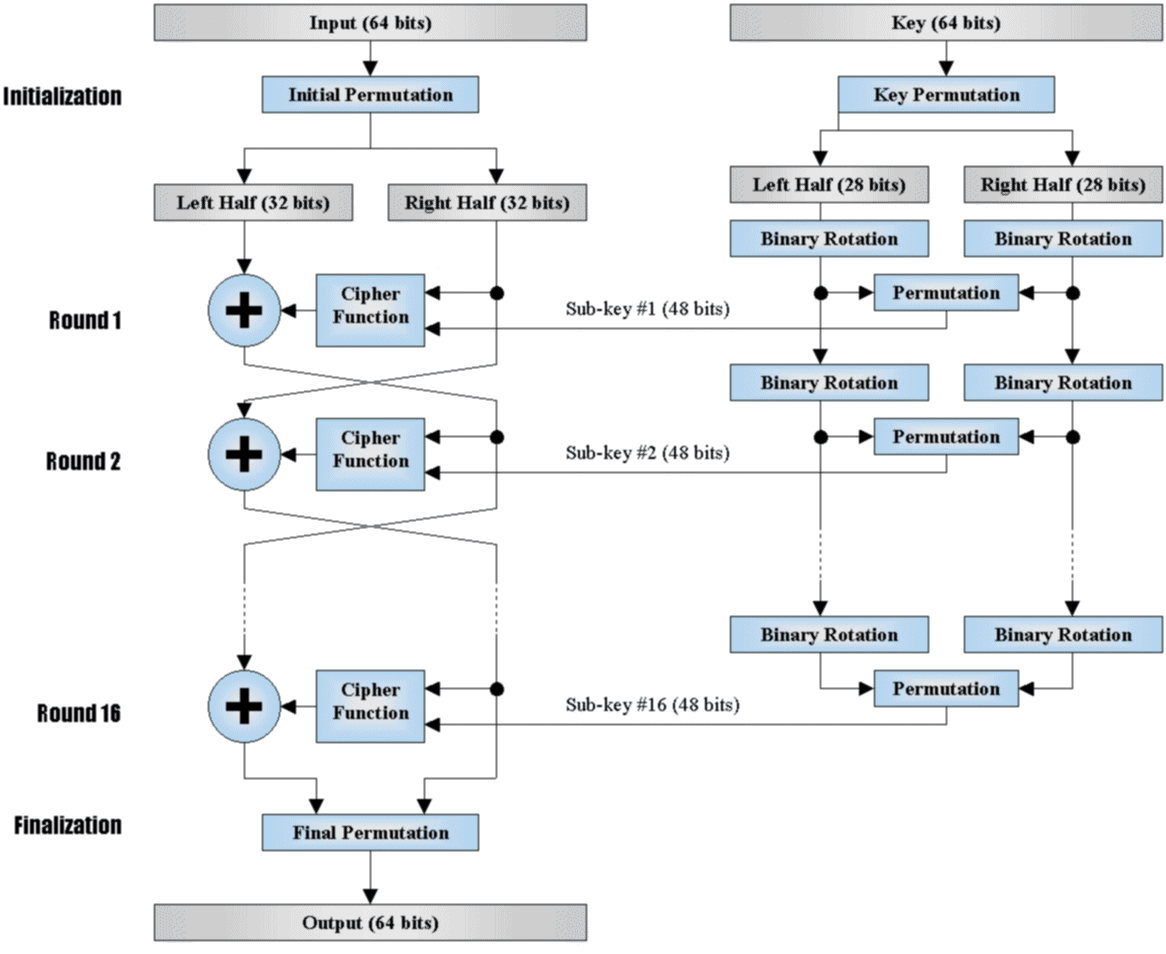
可以看到，整个算法可以看成是两个部分

密钥调度计算（右边基于给定密钥生成子密钥的过程）

所谓密钥调度，就是从一把64位的主密钥，得到16把48位的子密钥，然后把这些子密钥参与到后续16轮迭代加密中。那么，如何从一把主密钥得到16把子密钥呢？
1. 首先是从64位的主密钥中通过选择置换1选取特定的56位，其余的位就作为检验位，不参与后续计算。于是我们现在手上有了一个56位的密钥
2. 接着把它分成左、右两个半密钥C0、D0，它们都是28位的密钥
3. 然后对C0和D0进行16轮的迭代，每轮迭代都包括以下步骤：
  - 左、右两个半密钥Cn、Dn都左旋（也就是循环左移。整个数组往左移，左边弹出去了的东西补到最右边去）一定位数得到Cn+1、Dn+1，这个左移的位数也是指定的。有些轮次是1位，有些轮次是2位
  - 把左、右半密钥拼起来成为Kn+1，再通过选择置换2得到Kn，就得到了这一轮生成的子密钥。这个置换是从56位的数组里面选取指定的48位。所以现在每一轮都可以生成一个48位的子密钥。（注意，步骤3并不改变左右半密钥）。
4. 最后，经过16轮迭代之后，就生成了16个48位的子密钥，这些子密钥被用于加密和解密数据
5. 解密过程中，除了子密钥输出的顺序相反外，密钥调度的过程与加密完全相同
迭代加密（左边的16轮迭代加密的过程）迭代加密就是由具体数据参与的主流程的加密逻辑，具体逻辑是
1. 输入的明文（64bit）做一个置换（IP置换）。仍然得到64bit的数组（位数不等会导致信息丢失）
2. 同样基于Feistel Network的概念将数据拆分成左右两个半数据，各32bit
3. 每轮迭代都是接收一组L、R，返回L’、R’，作为下一轮迭代的 L, R . 迭代过程如下：
  text
```
L' = R
R' = L⊕F(R,subkey)
```
  关键在于F函数，也称为轮（Round）函数，是整个算法的核心，用于以子密钥加密32bit的信息
4. 步骤3执行16轮，每轮分别更新L、R值
5. 将最终得到的L、R值进行合并，再做一次置换（FP置换），即可得到密文

以上就是DES算法的大致过程，文中也提到，加解密的唯一区别就在于子密钥的顺序不同

1 密钥调度计算

详细来看看DES如何通过给定的主密钥而生成16把子密钥的，图示如下：

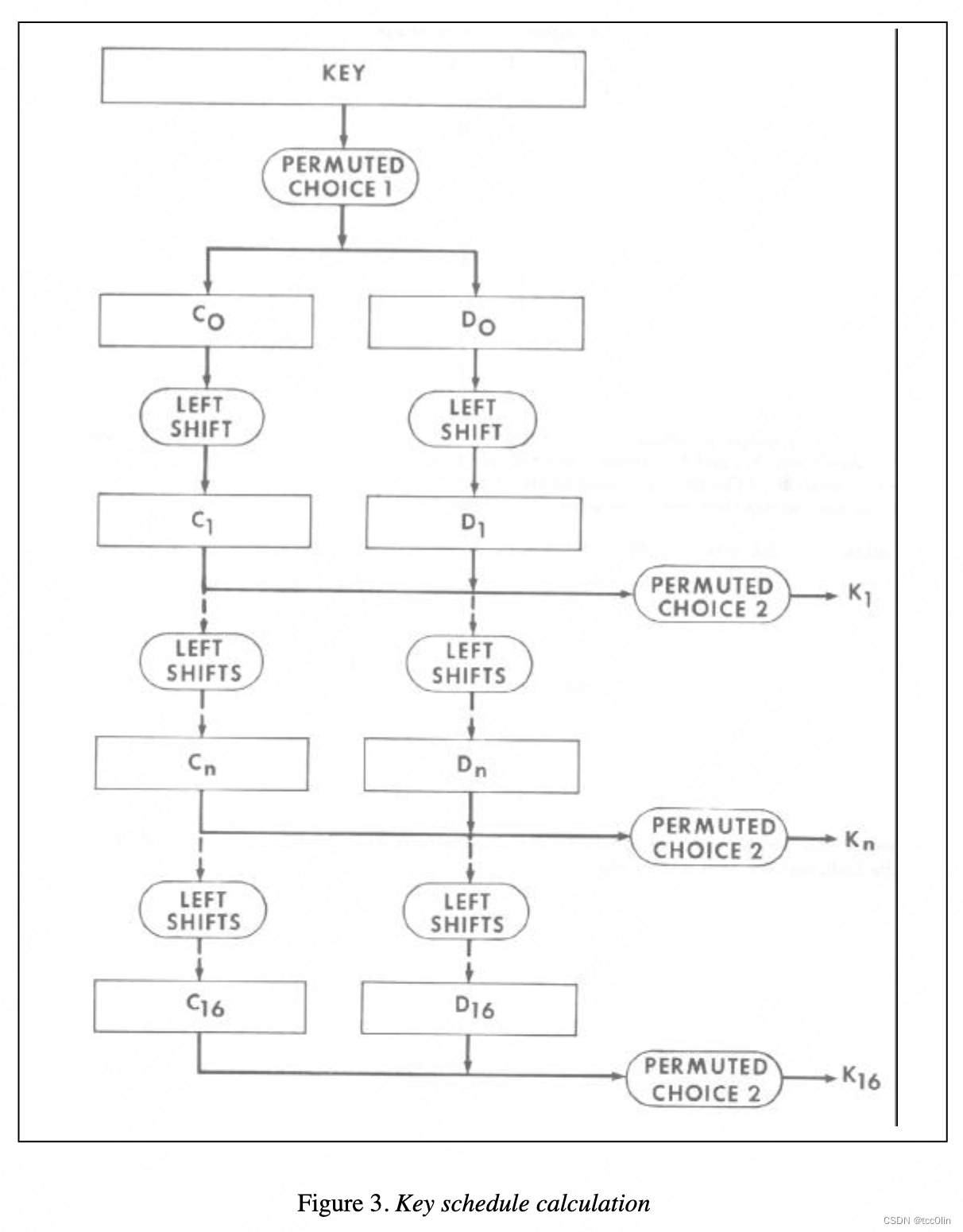
首先，采用“选择置换1 (PC-1)”，从64位key里面选出56位。这一步属于encode，对信息安全没有帮助。PC-1方法如下：

const int pc_1[56] = {  57 ,49 ,41 ,33 ,25 ,17 ,9  ,
    1  ,58 ,50 ,42 ,34 ,26 ,18 ,
    10 ,2  ,59 ,51 ,43 ,35 ,27 ,
    19 ,11 ,3  ,60 ,52 ,44 ,36 ,
    63 ,55 ,47 ,39 ,31 ,23 ,15 ,
    7  ,62 ,54 ,46 ,38 ,30 ,22 ,
    14 ,6  ,61 ,53 ,45 ,37 ,29 ,
    21 ,13 ,5  ,28 ,20 ,12 ,4 };
string key_56 = "";
for (int i = 0; i < 56; i++)
    key_56 += key_64[pc_1[i] - 1];

经过PC-1之后，我们有了左、右两个半密钥，长度都是28位。接下来，我们每一轮把左、右半密钥左旋几位，再调用PC-2方法来造子密钥。框架如下：

int num_leftShift[16] = { 1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1 }; 
L_key[0] = shift_bit(key_firstHalf, num_leftShift[0]); 
R_key[0] = shift_bit(key_secondHalf, num_leftShift[0]);
for (int i = 1; i < 16; i++)
{
    L_key[i] = shift_bit(L_key[i - 1], num_leftShift[i]);
    R_key[i] = shift_bit(R_key[i - 1], num_leftShift[i]);
}
for (int i = 0; i < 16; i++)
{
    keys_56[i] = L_key[i] + R_key[i]; // making 56 bits keys
}

其中， shift_bit是循环左移，实现如下：

string shift_bit(string s, int n)
{
    string k = "";

    for (int i = n; i < s.size(); i++)
        k += s[i];

    for (int i = 0; i < n; i++)
        k += s[i];

    return k;
}

PC-2又是一个简单置换，用于从左右半密钥拼起来的56位密钥中，选取48位作为一个子密钥。实现如下：

const int pc_2[48] = {  14 ,17 ,11 ,24 ,1  ,5  ,
    3  ,28 ,15 ,6  ,21 ,10 ,
    23 ,19 ,12 ,4  ,26 ,8  ,
    16 ,7  ,27 ,20 ,13 ,2  ,
    41 ,52 ,31 ,37 ,47 ,55 ,
    30 ,40 ,51 ,45 ,33 ,48 ,
    44 ,49 ,39 ,56 ,34 ,53 ,
    46 ,42 ,50 ,36 ,29 ,32 };
for (int i = 0; i < 16; i++)
{
    key_48[i] = "";
    for (int j = 0; j < 48; j++)
        key_48[i] += keys_56[i][pc_2[j] - 1]; // making 48 bits keys
}

这样，我们就实现了密钥调度算法。基于主密钥而得到的16个48位的子密钥。不难看出，整个密钥调度的过程都是对主密钥的encode。生成这么多子密钥的目的，是使得加密迭代变得更加复杂、难以分析

2 迭代加密

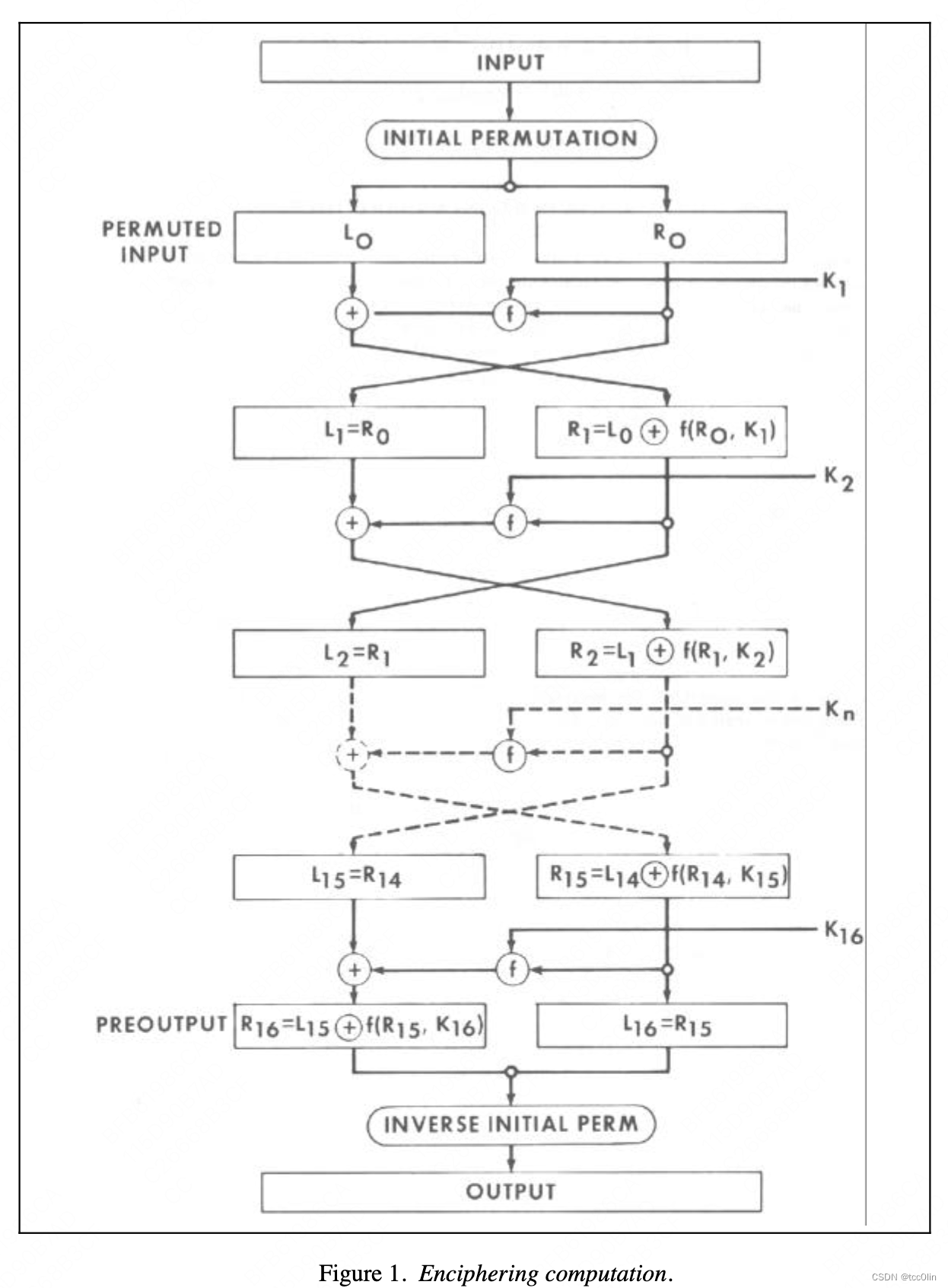加密迭代的过程已经描述过。先把信息进行一次初始置换(IP置换)；再进行16轮迭代；最后再给(R+L)这个数组来一次最终置换(FP置换)，即可输出作为密文

const int IP_t[64] = { 	58 ,50 ,42 ,34 ,26 ,18 ,10 ,2 ,  
    60 ,52 ,44 ,36 ,28 ,20 ,12 ,4 ,
    62 ,54 ,46 ,38 ,30 ,22 ,14 ,6 ,
    64 ,56 ,48 ,40 ,32 ,24 ,16 ,8 ,
    57 ,49 ,41 ,33 ,25 ,17 ,9  ,1 ,
    59 ,51 ,43 ,35 ,27 ,19 ,11 ,3 ,
    61 ,53 ,45 ,37 ,29 ,21 ,13 ,5 ,
    63 ,55 ,47 ,39 ,31 ,23 ,15 ,7 };

string IP = ""; // permuted key
for (int i = 0; i < 64; i++)
    IP += plain_txt_64[IP_t[i] - 1];

DES的安全性在很大程度上取决于F函数，也就是轮函数。那么Feistel函数是干了什么事呢？来看下面一张流程图：

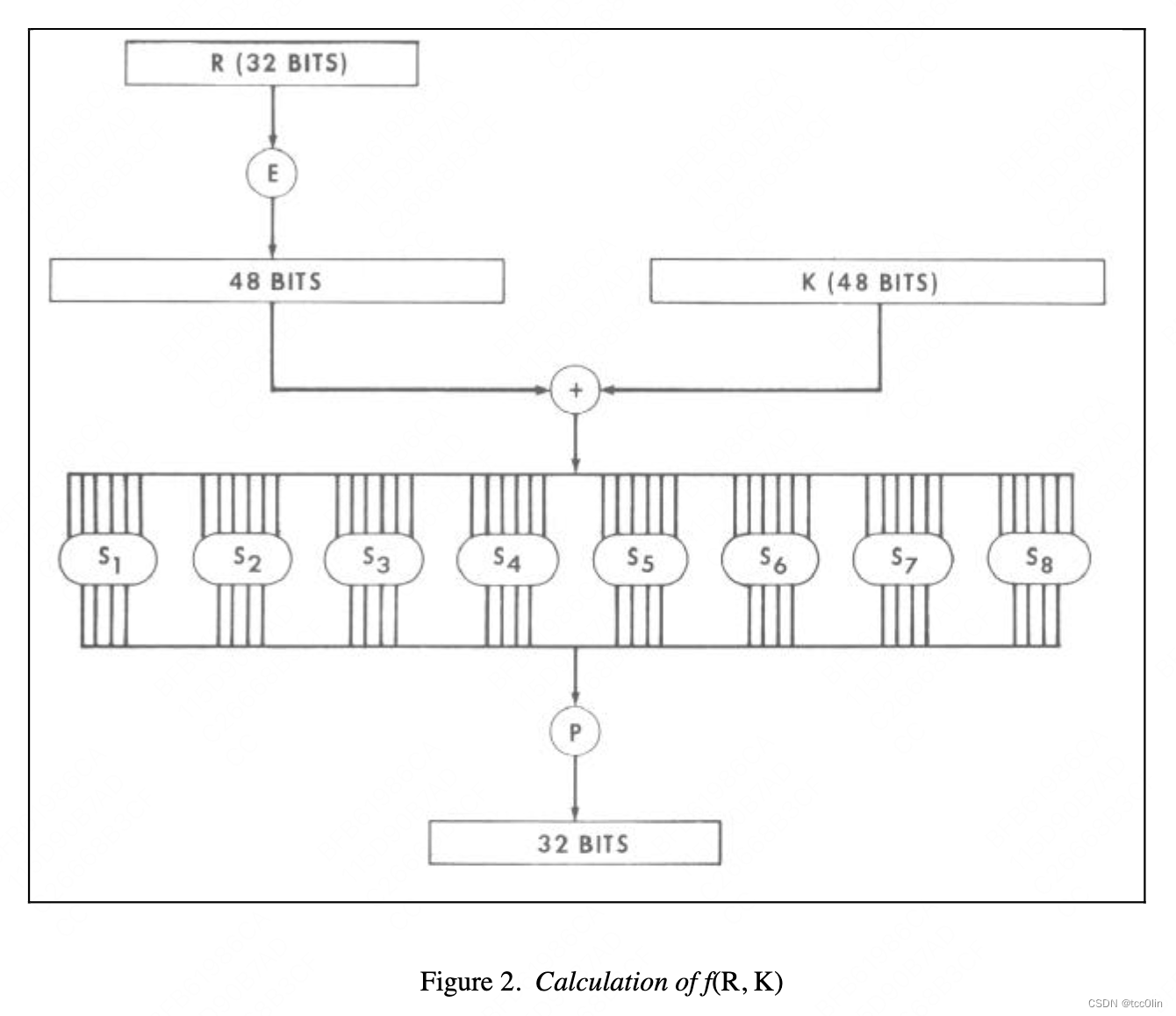
一个32-bit的块，经过一个扩张(Expand函数)，变成48位，然后与子密钥异或。得到的48-bit的结果分为8组，每一组是6-bit的数据，丢进对应的S盒，输出4-bit的信息。把这些输出收集起来，一共是4*8=32位，做一次置换(P置换)，得到32-bit的结果。这与输进来的32-bit信息是等长度的。

Expand算法是指定的

const int E_t[48] = { 	32 ,1  ,2  ,3  ,4  ,5  , // expantion table
    4  ,5  ,6  ,7  ,8  ,9  ,
    8  ,9  ,10 ,11 ,12 ,13 ,
    12 ,13 ,14 ,15 ,16 ,17 ,
    16 ,17 ,18 ,19 ,20 ,21 ,
    20 ,21 ,22 ,23 ,24 ,25 ,
    24 ,25 ,26 ,27 ,28 ,29 ,
    28 ,29 ,30 ,31 ,32 ,1 };
R_48[0] = "";
for (int j = 0; j < 48; j++)
    R_48[0] += R[E_t[j] - 1];

string xor_add(string s1, string s2)
{
    string result = "";
    for (int j = 0; j < s1.size(); j++) {
        if (s1[j] != s2[j]) result += '1';
        else result += '0';
    }
    return result;
}

R_xor_K[0] = xor_add(R_48[0], key_48[0]);

分成8组分别进入S盒处理

for (int j = 0; j <48; j += 6) // dividing each value of R_xor_K to 8 string contaning 6 char each
    for (int k = j; k < j + 6; k++)
        s[0][j / 6] += R_xor_K[0][k];

s_1[0] = "";
for (int j = 0; j < 8; j++)
    s_1[0] += get_element_from_box(s[0][j], j);

S盒构成如下

int S[8][4][16] = {                        // S-box
		{
			{ 14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7 },
			{ 0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8 },
			{ 4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0 },
			{ 15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13 }
		},
		{
			{ 15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10 },
			{ 3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5 },
			{ 0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15 },
			{ 13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9 }
		},
		{
			{ 10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8 },
			{ 13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1 },
			{ 13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7 },
			{ 1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12 }
		},
		{
			{ 7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15 },
			{ 13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9 },
			{ 10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4 },
			{ 3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14 }
		},
		{
			{ 2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9 },
			{ 14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6 },
			{ 4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14 },
			{ 11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3 }
		},
		{
			{ 12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11 },
			{ 10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8 },
			{ 9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6 },
			{ 4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13 }
		},
		{
			{ 4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1 },
			{ 13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6 },
			{ 1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2 },
			{ 6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12 }
		},
		{
			{ 13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7 },
			{ 1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2 },
			{ 7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8 },
			{ 2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11 }
		}
	};

string get_element_from_box(string s, int k)
{
    int dec1 = 0, dec2 = 0, pwr = 0;
    dec1 = (int)(s[0] - '0') * 2 + (int)(s[5] - '0');
    for (int i = s.size() - 2; i >= 1; i--)
    {
        dec2 += (int)(s[i] - '0') * pow(2, pwr++);
    }

    return Dec_to_Bin(S[k][dec1][dec2]);
}

S盒变换的逻辑参考：

text

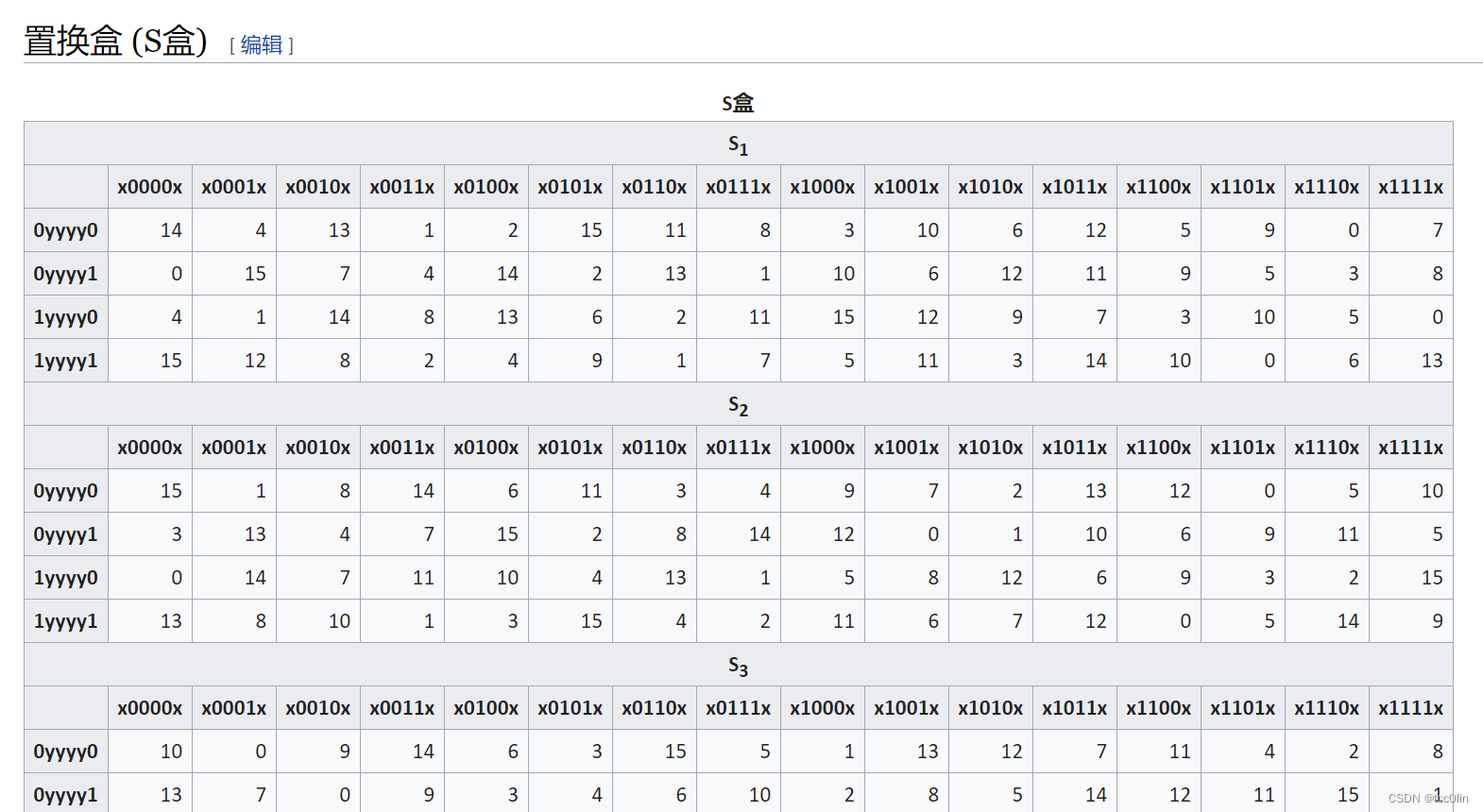
现在我们假设第二组是 101100 ，来看它在 S盒变换之后会得到什么结果
由于这是第二组，故查询 S2 表。
它的首位、末尾是 10 ，故查询第三行(1yyyy0行)。
它的中间 4 位是 0110 ，查表知结果是 13.
把 13 转为二进制，得到 1101 ，于是这就是输出

最后得到的32位结果还需要经过一个P置换

const int P[32] = { 	16 ,7  ,20 ,21 ,
    29 ,12 ,28 ,17 ,
    1  ,15 ,23 ,26 ,
    5  ,18 ,31 ,10 ,
    2  ,8  ,24 ,14 ,
    32 ,27 ,3  ,9  ,
    19 ,13 ,30 ,6  ,
    22 ,11 ,4  ,25 };
for (int j = 0; j < 32; j++)
	P_R[0] += s_1[0][P[j] - 1];

三、理解

DES也算是第一代的公认的对称加密的标准算法，核心在于F函数的概念与实现。当然DES算法主体流程还是依赖于固定64位的输入输出，而到了实际使用上还存在有不同的工作方式以及安全性问题，这些问题还等到后续继续补充

目录

目录

从FIPS 46-3中理解DES算法

一、DES概述

二、DES算法框架

1 密钥调度计算

2 迭代加密

三、理解