理解CRC32算法
一、CRC算法概述
循环冗余校验(Cyclic Redundancy Check, CRC)是一种根据网络数据包或计算机文件等数据产生简短固定位数校验码的一种信道编码技术,主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的原理来作错误侦测的。 ––维基百科
在对信息的处理过程中,我们可以将要被处理的数据块M看成一个n阶的二进制多项式,其形式如下
$M=a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+a_{n-3}x^{n-3}+……+a_1x^1+a_0$
CRC校验就是基于这种多项式进行的运算,以GF(2)(The integers modulo 2)多项式算术为数学基础,即(模-2)除法的余数运算(其实说白了就是异或Xor),使用的除数不同,CRC的类型也就不一样。CRC传输实际上就是在长度为 k 的数据后面添加供差错检测(Frame Check Sequence) 用的 r 位冗余码(Redundant code 没错CRC里面的R就是这个),使原数据构成 n = k + r 位并发送出去, 此方式又叫(n, k)码。可以证明存在一个最高次幂为n-k=r的多项式G(x), 根据G(x)可以生成k位信息的校验码,而 G(x) 叫做这个CRC码的生成多项式( Poly )。而根据 k 值的不同,就形成了不同的CRC码的生成多项式,以下为各种常用的多项表达式:
$crc-4=x^4+x+1$
$crc-8=x^8+x^5+x^4+1$
$crc-32=x^32+x^26+x^2+x^22+x^16+x^12+x^11+x^10+x^8+x^7+x^5+x^4+x^2+x^1+1$
这些多项表达式的值便是(模-2)除法的除数,这里选取CRC-32多项式(即为对应除数)格式,通过取余做操,获取CRC检验码
二、CRC32算法框架
CRC32校验计算框架如下:
- 选择一个生成多项式G(x)
- 假设该生成多项式G(x)的二进制数有k位,在发送的数据帧B(x)(设为m位)后加k-1个0,得到新二进制串H(x),H(x)位数应该为m+k-1。
- H(x)“模2除法”除以G(x),所得到的余数(记为F(x))就是原数据帧的CRC校验码,又称FCS(帧校验序列)。注意,F(x)的位数只能比G(x)少一位,0不能省略。
- 将F(x)附加到B(x)后面,组成新帧N(x),然后发送到接收端。
- 接收端将N(x)以“模2除法”除以G(x),如果没有余数,则表明没有出错(因为在发送端发送数据帧之前就已附加了一个数,做了去余处理(也就已经能整除了),所以结果应该没有余数。如果有余数,则表明该帧在传输过程中出现了差错)。
1 多项式选择
如上面所示,常见CRC标准如下
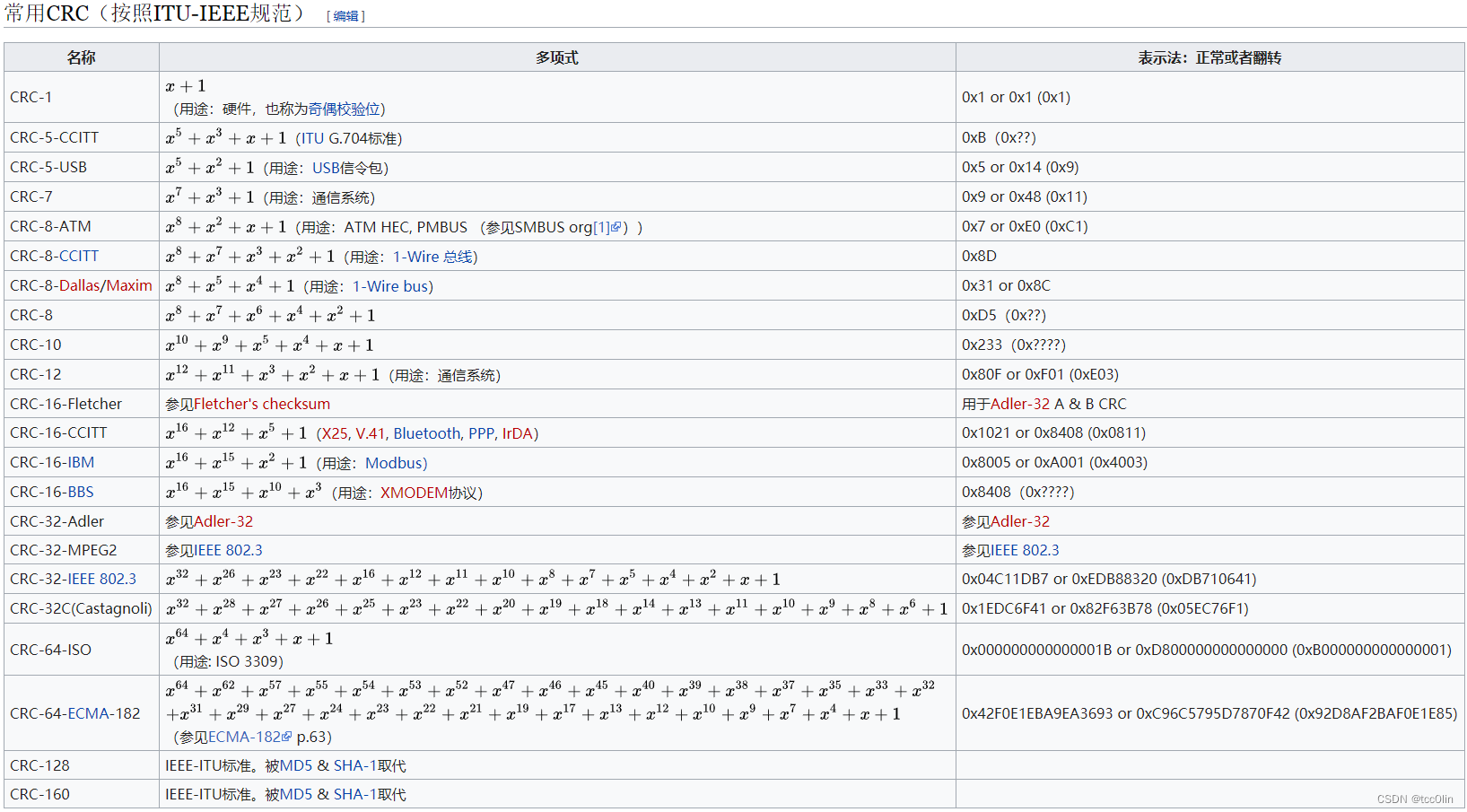 通常多项式也会使用二进制来表示,计算方式是x的最高幂次对应二进制数的最高位,以下各位对应多项式的各幂次,有此幂次项对应1,无此幂次项对应0。可以看出:x的最高幂次为R,转换成对应的二进制数有R+1位
通常多项式也会使用二进制来表示,计算方式是x的最高幂次对应二进制数的最高位,以下各位对应多项式的各幂次,有此幂次项对应1,无此幂次项对应0。可以看出:x的最高幂次为R,转换成对应的二进制数有R+1位
2 模2除法
CRC校验是基于多项式进行的运算,其加减法运算以2为模GF(2) ,加减时不进(借)位,实际上与逻辑异或(XOR)运算是一致, XOR是将参加运算的两个数据,按二进制位进行“异或”运算。
异或运算规则(^)规则如下:
0^0=0; 0^1=1; 1^0=1; 1^1=0;即:参加运算的两个对象,如果两个相应位为“异”(值不同),则该位结果为1,否则为0。
3 计算示例
以$G(x)=x^4+x^3+1$为例,设原数据为10110011
- $G(x)=x^4+x^3+1$, 二进制比特串为11001。(在X的n次方不为0处2的n次方的位=1)
- 因为校验码4位,所以10110011后面需加4个0,得到101100110000,用“模2除法” (即逻辑亦或^) 即可得出结果:

- 即CRC^101100110000得到101100110100,并发送到接收端
- 接收端收到101100110100后除以11001(以“模2除法”方式去除),余数为0则无差错
4 CRC的实现方式
一般来说CRC有多种实现方式,通常有直接生成法和查表法两种
直接生成法 适用于CRC次幂较小的格式,当CRC次幂逐渐增高时,因为其复杂的XOR逻辑运算会拖累系统运行速度,不再建议使用直接生成法,取而代之的是查表法——将数据块M 的一部分提前运算好,并将结果存入数组中,系统开始执行运算时,相当于省去了之前的操作,直接从类似中间的位置开始计算,所以会提高效率
生成CRC码表的方式如下:
int make_crc32_table()
{
uint32_t c;
int i = 0;
int bit = 0;
for(i = 0; i < 256; i++)
{
c = (uint32_t)i;
for(bit = 0; bit < 8; bit++)
{
if(c&1)
{
c = (c >> 1)^(0xEDB88320);
}
else
{
c = c >> 1;
}
}
uiCRC32_Table[i] = c;
}
}三、思考
如上面所理解的那样,CRC算法关键在于码表,但是码表也分动态生成和静态表,若是动态生成表,则应留意生成多项式,若是静态表,则会在数据段留下整个表